Game theory blockchain applications can help you understand how decentralized cryptoeconomic systems work without falling victim to internal disintegration and cheating. Game theory is a study of mathematical models of strategic interaction and decision-making between rational decision-makers. 

While game theory can be both cooperative and non-cooperative, we will be looking exclusively into the latter since a decentralized, cryptoeconomic environment is, by design, a trustless and non-cooperative one.

Your typical game theory model has three components:

• Players: The ones who make all the decisions. Eg. A company’s board of directors.
• Strategies: The decisions that the company will make to further its agenda.
• Payoff: Outcome of the strategies that have been made by the players.

First devised by John von Neumann and Osker Morgenstern in 1944, game theory was a significant breakthrough in the study of oligopoly markets. 

What is Oligopoly?

Market structure is the organizational and fundamental characteristics of a particular market. Based on a variety of different factors like the number of producers, control over prices and barriers to entry, these structures are divided into the following four categories:

• Perfect Competition 
• Monopoly
• Monopolistic Competition
• Oligopoly.

#1 Perfect Competition

Imagine your kid’s lemonade stand.

This is an example of perfect competition. Anyone can enter the market, and the individual sellers don’t have any power over the product’s price. If little Johnny decides to raise the price of his lemonade to 30 cents, his customers will simply go to Mary, who sells hers for 25 cents. 

Monopoly

The polar opposite of a “perfect competition” market structure is the monopoly structure. In a monopoly, one entity dominates the market. The barrier to entry is often so high that it is infeasible for someone new to enter the market anyway.

Think of Xerox. Is there a better example of a monopolistic sector than the “photocopy” space? Similarly, De Beers is another example of a company that has a monopoly over their market – diamonds.

Monopolistic Competition

Monopolistic competition is a marketplace that has a lot of sellers and a shallow entry barrier. The products sold by the competitors are also similar but not identical. Think of the doughnut industry. We have Dunkin Donuts, Krispy Kreme, Tim Hortons, etc. All of them have a product that is similar to slight subtle differences in taste and appearance. 

Usually, their products are roughly in the same price range and don’t have much leeway. If Dunkin Donuts start overcharging, people will simply go to Krispy Kreme or Tim Hortons. If all three of them start overcharging, a new player may enter the market due to the low barrier-to-entry.

Oligopoly

Oligopolies are similar to Monopolistic Competition but with one little difference. The barriers to entry in an oligopoly are incredibly high.  

One of the best examples of an oligopoly is the high-end wristwatch market. Companies like Rolex, Breitling, Patek Philippe, etc., dominate this market. The products are similar but not identical. However, this doesn’t give them total control over the market. Eg. If Rolex shoots up the price of their Submariner model to $10,000, only the Rolex fanatics will stick with the company. Everybody else will go for some other brand.

How can these products increase their product price without losing their customers to the competition? They can obviously get together and plan on increasing the price of the products as a whole. However, this is supposed to be highly illegal.

The only option they have is game theory.

The Need for Game theory

Classical economics fails to account for imperfect competition. Game theory enables you to model competing behaviors between different agents. Companies usually face multiple strategic choices that affect their overall output. They may have to make decisions regarding:

• Stopping the production of an existent product.
• Developing a new product.
• Lower the price of a product relative to the competition.
• Employing new marketing strategies.

Like we have said before, companies can’t just get together and decide how to price their products since that will be collusion. The only way that they can effectively compete is via non-price competition. The most recognizable form of non-price competition is advertising.

So, let’s create a payoff matrix to know whether or not two companies, A and B, can benefit from advertising or not.

So, we have two choices, either advertise or don’t advertise. According to the information given in our matrix:

• If one firm advertises and the other doesn’t the former stands gain a lot of payoff, while the other doesn’t.
• If they both advertise, then they both stand to gain quite a bit.

Looking into this payoff matrix, we can see that it’s in the interest of both the companies to advertise. In the example above, (4,3) is our Nash equilibrium.

What – What is the Nash equilibrium?

The famous mathematician, John Forbes Nash Jr, came up with a solution for a non-cooperative game involving two or more players called “Nash Equilibrium.” Yes, this is the same John F Nash, who was portrayed by Russell Crowe in the movie, “A Beautiful Mind.” 

In a non-cooperative game situation, the Nash equilibrium is considered the ideal solution for the two participants involved. In this state, both have something to gain from the payoff. Deviating from the equilibrium will lead to a loss in payoff for one or both of the participants.

Now that we have a brief idea of how it works let’s look into one of the most well-known concepts in game theory – The Prisoner’s Dilemma.

The Prisoner’s Dilemma

The Dark Knight had an exciting scene towards the end of the movie. The Joker had rigged two ferries with explosives. One ferry was full of innocent citizens and the other full of criminals. Each ship had a controller that blew the other one up. The Joker then announced this:

• They will need to blow the other ship up before a given time limit.
• If the time limit expires, then the Joker will blow both the ships up.

This is a classic example of the “Prisoner’s Dilemma” game. The idea was initially created by Merrill Flood and Melvin Dresher while working at RAND in 1950. 

The prisoner’s dilemma is a hypthetical scenario where two entirely rational individuals may not cooperate, even if it is in their best interest to do so. In the movie, both the prisoners and the citizens decided not to blow up the other’s ship in a pretty touching example of the innate goodness of human beings. They did this even though:

• They didn’t know if the other ship was going to blow them up or not.
• The Joker said that if none of the ships had exploded by the given time limit, he would blow both of them up.

Obviously, nothing happened because Batman ended up saving the day, but in reality, you can’t expect a ripped billionaire wearing a Halloween costume to keep you from making bad decisions.

So, let’s put this dilemma under the microscope with another example.

Image Credit

Suppose Alice and Bob got arrested for stealing a bank. Currently, their interrogation is taking place in separate rooms. The police gives them the following propositions:

• If either of them doesn’t rat the other one out, they will both get 5 years in prison
• However, if one rats the other out, they will be scot-free while the other one gets 7 years in prison.
• If both of them rats the other one out, they both get a 3-year sentence

The payoff matrix of this scenario looks like this:

Idealistically speaking, both Alice and Bob will not want to confess. However, game theory tells us that it may not be the most realistic scenario. Both Alice and Bob face far better payoffs if they rat on the other person. From Alice’s point of view, she gets:

• 0 years if Bob doesn’t confess.
• 3 years if Bob does confess.

Both of these two options are far better than the 5 years she will get if she doesn’t confess. She also risks getting a 7 year-sentence if Bob does confess. So, in this scenario, it is in both of their best interest to rat the other person out. Hence Nash equilibrium lies at (3,3).

Prisoner’s Dilemma with Punishment Factor

Now, let’s look at the moral implication of the equilibrium. What if the optimal payoff of a matrix is detrimental to society? Consider the following payoff matrix. Alice and Bob are deciding whether or not to rob a bank:

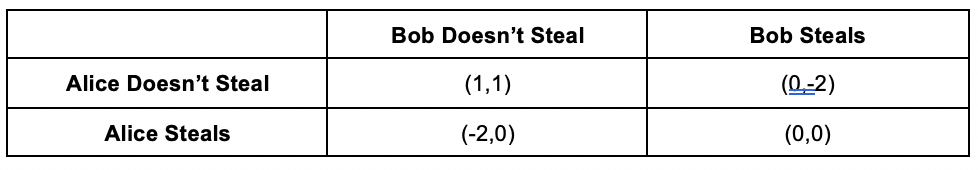
The payoff is the highest when both Alice and Bob steal together because it will be much more efficient. So, Nash equilibrium lies in both of them robbing the bank. Hmmm… this doesn’t look good. If this condition is valid for all similar payoff matrices, wouldn’t our society fall into complete madness? This is why we, as a society, have introduced a “punishment” factor to mitigate this chaos.

How does Punishment Work?

As opposed to what happened in The Dark Knight, people may not always choose to do the right thing. Human beings are, unfortunately, prone to corruption. Implementing a punishment factor to the payoffs will help keep the society in check.

In the example above, let’s imagine that the punishment factor works like this: 

“For every action taken against the public interest, a punishment factor of -7 will be given.” 

Now our payoff matrix looks like this. Every harmful action’s payoff reduces by a factor of 7:

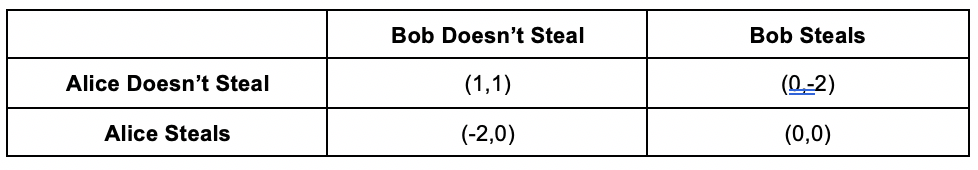
The payoffs have now changed considerably. Thanks to our punishment factor, it is now in Alice’s and Bob’s best interests to not steal, and (1,1) becomes our Nash Equilibrium.

The Schelling Point

Think of a popular pub in your town where people go to relax following a grueling day at work. The chances are that you just simply bump into your friends and colleagues at the bar. You don’t need to text them beforehand to coordinate. This is because the bar happens to be a Schelling Point for your colleagues.

So, what’s a Schelling Point? It is a solution that people will automatically use in the absence of proper communication. The answer is usually a value that’s special to them and feels natural/distinct. 

Let’s understand this with another example. Suppose we have two people in two different rooms. They both have to go through a series of numbers and guess what the other person will choose. The numbers given are – 7241, 5467, 1, and 8723.

What number do you think they are most likely to choose? Probably “1,” right? It feels natural to choose it since it’s quite different than the other numbers given in the list.

Bounded Rationality

The next concept that we are going to look into is Bounded Rationality. Consider this example.

You go to a grocer’s shop every single day and buy an apple. You did it every single day without fail, like a ritual. However, every time you do so, you face a weird scenario. Every day, for a couple of mins, the shopkeeper leaves to finish an errand. The shop is pretty old-school, so it doesn’t have any security camera in place. You can easily shoplift an apple, and nobody will get to know about it. 

However, you don’t do that. This is an example of bounded rationality. 

Bounded rationality states that the rationality of our decisions will be within the confines of the information available to us and our mental capacity.

In simple terms, people are always going to make decisions that are natural to them and don’t require many complications. Now, keep in mind that “simple” doesn’t always mean “right.” The decision need not yield the highest rewards, and it may not be best suited for them, but it is still something that will come naturally to them.

Let’s take another example of this – cryptocurrency trading.

The crypto market is highly volatile, and there is just way too much information to process for a normal human being. It is near impossible for someone to make a thoroughly educated and prudent decision given various time and intellectual limits. More often than not, people go by previous experience or the judgment of somebody else that they trust. 

Instead of taking into account all the different factors and making a super educated decision that positively affects their income, the majority of the investors simplify their decision-making and get an optimal result, which may not be the best one. Hence trading is an example of bounded rationality.

Grim Trigger Equilibrium

The next concept that we are going to look into is the “Grim Trigger Equilibrium.” In ancient times, one of the most common rules in place was the “divine right of kings.” People believed that certain individuals and their families are chosen by the Gods to rule over the masses. As such, the king is often considered a divine being.

Now, what happens if someone were to murder the king in cold blood?

Since the king’s mortality is exposed, the king’s divine right disappears. The moment that happens, the enter society descends into chaos. Once the king seems killable, it starts an endless cycle of bloodshed where future kings keep getting murdered by usurpers or the disgruntled public.

The only way to stop it is not to begin it in the first place. By not killing the original king, you maintain the idea of a “divine right.” This is called a “Grim Trigger Equilibrium.” A Grim Tigger is a state of equilibrium where a slight deviation leads to an endless cycle of recursive punishment.

Coordination Game

Take a look at this matrix:

 A

 B

A

 (10,10)

 (0,0)

B

 (0,0)

 (10,10)

This matrix has two Nash Equilibria: (A, A) and (B, B). The two players can choose any of them and still get an equal payoff. Let’s also imagine that (A, A) is the most popular choice for now. The question is, how do we move our equilibrium from (A,A) to (B,B). 

This particular scenario is critical for a WAN like Bitcoin. A small group of people can easily coordinate with each other via phone and email. However, a purposefully decentralized network like Bitcoin will have a hard time properly coordinating with each other. So, if there is an upgrade in the system, how do we ensure that the community can jump from one protocol to another without having to connect with each other individually?

The solution here is to convince a majority of the network to switch the protocol, while the rest will follow. Let’s understand how this works with a simple example. Imagine that there is a hot new messaging app in the market. If nearly all of your friends move on to the new app, you will want to download it as well, right? After all, you don’t want to miss out on the fun.

The same logic works for a decentralized protocol as well. If a majority of the network organically moves on to the new protocol, the rest of the nodes will eventually move forward because they don’t want to be left out of the loop.

Proof of Work Game Theory

Let’s look at how these different game theory principles mitigate attack scenarios in a blockchain. A blockchain is a series of linked blocks containing timestamped data.

The Bitcoin blockchain follows a consensus model called “proof-of-work.” In this model, we have certain participants called miners, who use their computational power to mine on the blockchain and create new blocks. The differences between a blockchain and other similar decentralized networks, such as the Tangle, are described in the article Blockchain vs Tangle.

The structure that you see above is a more idealistic version of the blockchain. In reality, it looks more like this:

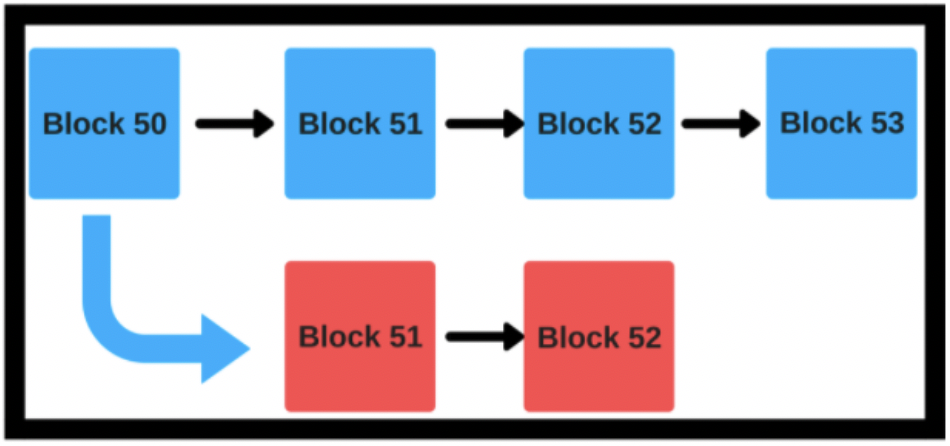
There are tens of thousands of sidechains attached to the main Bitcoin blockchain. To avoid any confusion and to prevent double-spending, the majority of the Bitcoin miners don’t tend to mine on these smaller sidechains. The reason for that is pretty simple. The longest chain in the Bitcoin network acts as a Schelling Point for Bitcoin miners. Mining on any of the other side chains ends up being a huge waste of resources as the transactions done on those chains are not considered to be of any real worth.

However, Ethereum founder Vitalik Buterin gave an interesting example of how someone can take over a proof-of-work system. If the attacker has enormous resources and enough motivation, they can theoretically take over a proof-of-work blockchain by using a bribery model or a “P+Epsilon attack.”

P+Epsilon Attack

To understand the “P+Epsilon” attack, look at this table. Let’s imagine that you are a miner and let’s see how your decisions wrt the other miners change your payoff:

We can make the following conclusions:

• If you make the same decision as the other miners, then you get a payoff.
• If your decision contradicts that of the other miners, you get no payoff.
• There are two Nash equilibriums in the matrix above.
• Choosing to stay on the chain or going to a different chain will require significant coordination.
• Coordination theory says that a good majority needs to transition to the next state to make the new scenario/chain work.

Now suppose we have an attacker with considerable resources. This attacker enters the network and individually approaches individual miners. He tells them that if they vote differently from the system, they will get a payoff of “P + ε.” The usual payoff and an extra bribe of ε on top of that. Now, our matrix looks like this:

Now, this leads to another unusual situation:

• If you choose to stay, then there is a 50-50 chance of you getting a payoff.
• If you choose to go on a different chain, you either get a payoff P or a payoff of P + ε, depending on what others have chosen.

You are obviously going to make a decision which guarantees some payoff. Hence you will choose to go to a different chain.

Now suppose this attacker has approached all the miners with this deal, then something fascinating happens. Since everyone votes to go on a different chain, the Nash Equilibrium shifts to:

So, the attacker was able to change the whole course of the network without needing to pay that extra bribe.

How can Game Theory mitigate the above scenario?

• As already mentioned, miners have an economic incentive to mine on the longest chain because it is the Schelling Point of the entire network.
• Users will value the main chain more since they are simply used to it. Like bounded rationality states, people will opt for the simplest solution every time. Moving through a newer chain complicates things.
• Bribing the network like this will shift the grim trigger equilibrium. What is going to stop future attackers to bribe the system again to change to a newer chain? To prevent this recursive punishment system, it is much better not to shift focus from the original main chain in the first place. 
• Finally, especially in the context of the Bitcoin blockchain, the network is so vast and decentralized, that it is infeasible for a briber to individually connect with the majority of the miners in an attempt to stage a coordination coup. Solving this coordination problem requires an absurd amount of resourcefulness, drive, and patience from the attacker.

Conclusion

Game theory prevents internal corruption and helps in rational decision-making for oligopolies and other economic structures. It is at the heart and soul of all financial and cryptoeconomic systems and is one of the most significant factors in maintaining its overall integrity. Those interested in game theory blockchain mechanics should make sure to also examine the Byzantine Generals’ Problem.